Metoda Falsi (zwana metodą fałszywych linii).
Darmowy hosting zapewnia PRV.PL
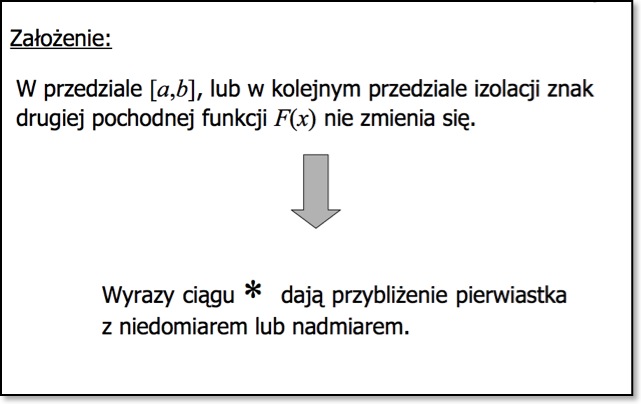
Założenia jakie muszą być spełnione:
1. W przedziale izolacji [a,b], w którym położony jest pierwiastek, funkcja f(x)=f(a)xF(b)<0 - posiada przeciwne znaki na krańcach przedziału.
2. Pierwsza i druga pochodna mają stały znak.
A tym samym spełnione są twierdzenia:
Twierdzenie 1. (Bolzano – Cauchy’ego)
Jeżeli funkcja F(x) jest ciągła w przedziale domkniętym [a,b] i F(a)⋅F(b) < 0, to między punktami a i b znajduje się co najmniej jeden pierwiastek równania F(x) = 0.
Twierdzenie 2.
Jeśli w przedziale [a, b] spełnione są założenia twierdzenia i dodatkowo sgn F ′(x) = const dla x∈[a,b], to przedział ten jest przedziałem izolacji pierwiastka równania F(x) = 0
Opis:
Metoda polega na znalezieniu przybliżonego pierwiastka. Aby go znaleźć musimy poprowadzić cięciwę przez punkty A(a,f(a)) i B (b, f(b)) .
Równanie cięciwy:
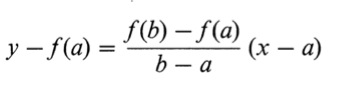
Odciętą punktu x1 przyjmujemy za pierwsze przybliżenie
:
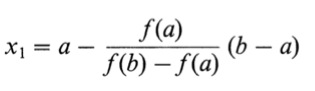
Jeżeli f(x1)=0 to x1 jest szukanym pierwiastkiem. Jeśli natomiast f(x1)<>0 to przez punkt C(x1,f(x1)) oraz przez jeden z punktów A lub B którego rzędna ma przeciwny znak niż f(x1)
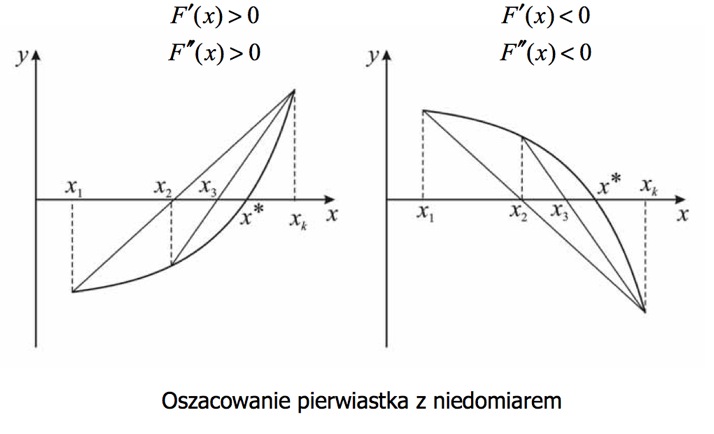
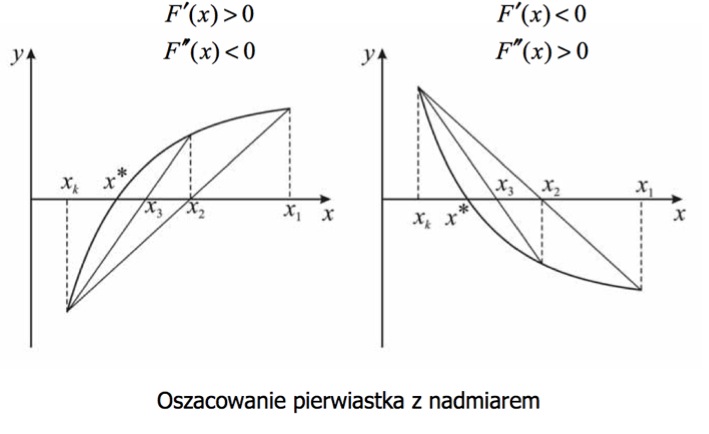
Przykładowe wykresy szukania pierwiastków
: